CA Foundation Equations and Matrices Summary

Equations and Matrices Summary Applicable for CA Foundation November 2020 Exams.

EQUATIONS

• A simple equation in one unknown x is in the form ax + b = 0. Where a, b are known constants and a ≠0
• The general form of a linear equations in two unknowns x and y is ax + by + c = 0 where a, b are non-zero coefficients and c is a constant. Two such equations a₁x + b₁y + c₁ = 0 and a₂ x + b₂ y + c₂ = 0 form a pair of simultaneous equations in x and y. A value for each unknown which satisfies simultaneously both the equations will give the roots of the equations.
• Elimination Method: In this method two given linear equations are reduced to a linear equation in one unknown by eliminating one of the unknowns and then solving for the other unknown.
• Cross Multiplication Method: Let two equations be:

a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂= 0

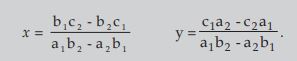
• An equation of the form ax² + bx + c = 0 where x is a variable and a, b, c are constants with a¹ ≠ 0 is called a quadratic equation or equation of the second degree.

When b=0 the equation is called a pure quadratic equation; when b = 0 the equation is called an affected quadratic.

• The roots of a quadratic equation:

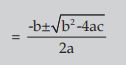
• The Sum and Product of the Roots of quadratic equation

• To construct a quadratic equation for the equation ax² + bx + c = 0 we have x² – (Sum of the roots) x + Product of the roots = 0
• Nature of the roots

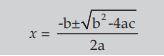
i) If b²–4ac = 0 the roots are real and equal;

ii) If b²–4ac >0 then the roots are real and unequal (or distinct);

iii) If b²–4ac <0 then the roots are imaginary;

iv) If b²–4ac is a perfect square ( ≠0) the roots are real, rational and unequal (distinct);

v) If b²–4ac >0 but not a perfect square the rots are real, irrational and unequal. Since b² – 4ac discriminates the roots b² – 4ac is called the discriminant in the equation ax² + bx + c = 0 as it actually discriminates between the roots.

Matrices

• General form matrix of order m × n is

• Only square matrices have determinates. A Determinant of n rows and n columns is called determinant of order n . General form of determinant of order n is

• Only matrices of the same order can be added or subtracted. To add (or subtract) two matrices, we add (or subtract) their corresponding elements.
• To multiply a matrix with a number, we multiply every element of the matrix with that number whereas to multiply a determinant with a number we multiply only one row (or column) of the determinant with that number.
• Two matrices can be multiplied only if the number of columns of the first is the same as the number of rows of the second, E.g. , a 2 × 3 matrix can be multiplied by a 3 × 4 matrix. The order of resulting matrix will be 3 × 4.
• Transpose of a matrix A is the matrix obtained by interchanging rows and columns of the matrix A. It is denoted by A’or A^T .
• Adjoint of matrix A is transpose of the co-factor matrix of A, e.g.,

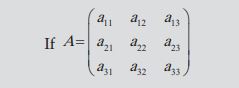
Let C₁₁ be co-factor of a₁₁ and so on